竞赛题：一元二次方程14。

今天讲解一元二次方程的竞赛题。看题，这个分式方程恰好有一个实数根，都知道出现了分数肯定要去分母，所以两边同乘，X(x-1)也就得到2kx2+3x-7=4kx-4k。先移顶、再合并同类项，也就是2kx2+(3-4k+4-7=0)。

题目说它是关于x的方程，不知道它是一元一次还是一元二次，所以就分类讨论。

·第一种：当它是一元一式方程的时候，说明二次项的系数：2k-0，解得k=0。代入可得，原式变成3x-7=0，那么x=7/3。

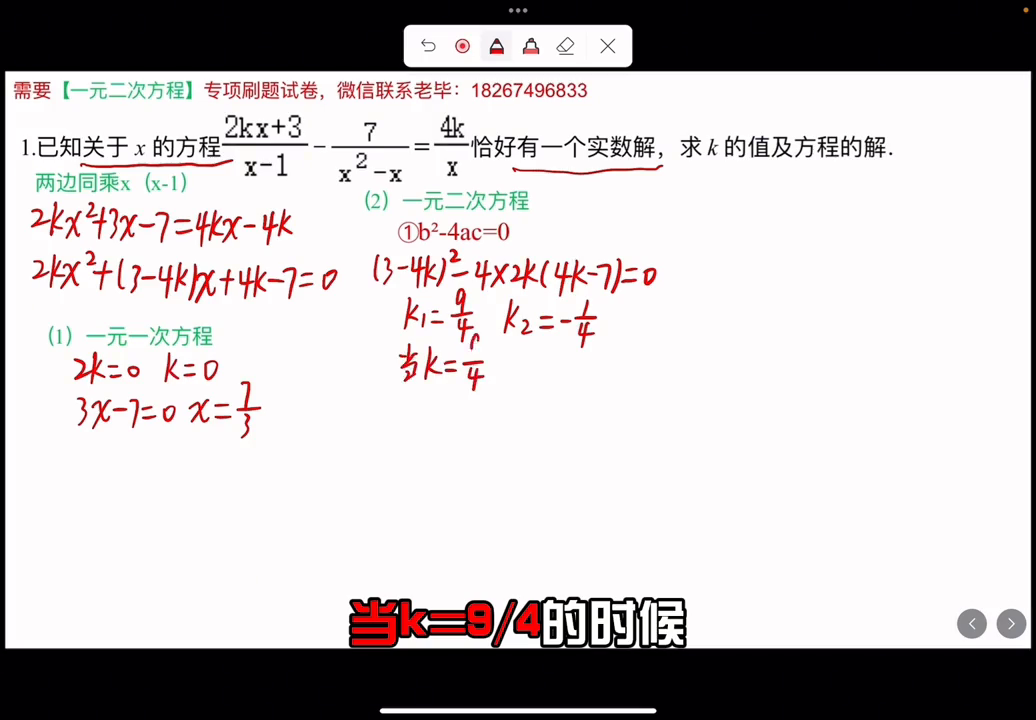
·第二种：它可以是一元二次方程，一元二次方程只有一个实数根，说明什么？说明b-4ac=0，所以(3-4k)2-8k(4k-7)=0，解得k=9/4，k2==1/4。当k-9/4的时候，把这个9/4代回原式，可以解得x=2/3。同理，当k=1/4的时候，解得x=4。

·第三种：当一元二次方程有两个根的时候，其中一个根是分式方程的增根，总的来说这个方程还是只有一个实数解。因为分式方程有增根，所以分母为0，即x=1或0。

→第一种：x=1，把这个1代入原式，可以得到：2k+3-4k-7=0，解得k-2。再把这个k=2代回来，就可以解得x=1/4。

→第二种：x=0，代入原式，可以得到：4k-7=0，k=7/4，代入可得：x=8/7。

-_a-2x只有一个实根，听懂同学把这题做出来吧。